The Continental Club in Austin, Texas, USA
Sunday, January 5, 1987
“Thank you for your kind invitation, Mr. Lomuto. I will soon return to England so this is quite timely.”
“And thanks for agreeing to meeting me, Mister… Sir… Charles… A.R… Hoare. It’s a great honor. I don’t even know how to address you. Were you knighted?”
“Call me Tony, and if it’s not too much imposition please allow me to call you Nico.”
On the surface, a banal scene—two men enjoying a whiskey. However, a closer look revealed a number of intriguing details. For starters, a tension you could cut with a knife.
Dressed in a perfectly tailored four-piece suit worn with the nonchalance only an Englishman could pull off, Tony Hoare was as British as a cup of tea. His resigned grimaces as he was sipping from his glass spoke volumes about his opinion of Bourbon versus Scotch. On the other side of the small table, Nico Lomuto couldn’t have been more different: a casually dressed coder enjoying his whiskey with Coca-Cola (a matter so outrageous that Tony had decided early on to studiously pretend not to notice, as he would when confronted with ripe body odor or an offensive tattoo), in a sort of relaxed awe at the sight of the Computer Science giant he had just met.
“Listen, Tony,” Nico said as the chit chat petered off, “about that partitioning algorithm. I never meant to publish or—”
“Oh? Yes, yes, the partitioning algorithm.” Tony’s eyebrows rose with feigned surprise, as if it had escaped his mind that every paper and book on quicksort in the past five years mentioned their names together. It was obviously the one thing connecting the two men and the motivation of the meeting, but Tony, the perfect gentleman, could talk about the weather for hours with a pink elephant in the room if his conversation partner didn’t bring it up.
“Yeah, that partitioning algorithm that keeps on getting mentioned together with yours,” Nico continued. “I’m not much of an algorithms theorist. I’m working on Ada, and this entire thing about my partition scheme is a distraction. The bothersome part about it”—Nico was speaking in the forthcoming tone of a man with nothing to hide—”is that it’s not even a better algorithm. My partitioning scheme will always do the same number of comparisons and at least as many swaps as yours. In the worst case, mine does n additional swaps—n! I can’t understand why they keep on mentioning the blessed thing. It’s out of my hands now. I can’t tell them what algorithms to teach and publish. It’s like bubblesort. Whenever anyone mentions quicksort, there’s some chowderhead—or should I say bubblehead—in the audience going, yes, I also heard of the bubblesort algorithm. Makes my blood curdle.”
Nico sighed. Tony nodded. Mutual values. Rapport filled the air in between as suddenly, quietly, and pleasantly as the smell of cookies out of the oven. A few seconds went by. Jack and Coke sip. On the other side of the table, Bourbon sip, resigned grimace.
Tony spoke with the carefully chosen words of a scientist who wants to leave no hypothesis unexplored. “I understand, Nico. Yet please consider the following. Your algorithm is simple and regular, moves in only one direction, and does at most one swap per step. That may be appropriate for some future machines that…”
“No matter the machine, more swaps can’t be better than fewer swaps. It’s common sense,” Nico said, peremptorily.
“I would not be so sure. Computers do not have common sense. Computers are surprising. It stands to reason they’ll continue to be. Well, how about we enjoy this evening. Nothing like a good conversation in a quiet club.”
“Yeah. Cheers. This is a fun place. I hear they’ll have live country music soon.”
“Charming.” Somewhat to his own surprise, Tony mustered a polite smile.
Chestnut Hill, Massachusetts, USA
Present Day
I’ve carried an unconfessed addiction to the sorting problem for many years. Wasn’t that difficult to hide—to a good extent, an obsessive inclination to studying sorting is a socially tolerated déformation professionnelle; no doubt many a programmer has spent a few late nights trying yet another sorting idea that’s going to be so much better than the others. So nobody raised an eyebrow when I wrote about sorting all the way back in 2002 (ever heard about “fit pivot?” Of course you didn’t). There was no intervention organized when I wrote D’s std.sort, which turned out to be sometimes quadratic (and has been thankfully fixed since). No scorn even when I wrote an academic paper on the selection problem (sort’s cousin) as an unaffiliated outsider, which even the conference organizers said was quite a trick. And no public outrage when I spoke about sorting at CppCon 2019. Coders understand.
So, I manage. You know what they say—one day at a time. Yet I did feel a tinge of excitement when I saw the title of a recent paper: “Branch Mispredictions Don’t Affect Mergesort.” Such an intriguing title. To start with, are branch mispredictions expected to affect mergesort? I don’t have much of an idea, mainly because everybody and their cat is using quicksort, not mergesort, so the latter hasn’t really been at the center of my focus. But hey, I don’t even need to worry about it because the title resolutely asserts that that problem I didn’t know I was supposed to worry about, I don’t need to worry about after all. So in a way the title cancels itself out. Yet I did read the paper (and recommend you do the same) and among many interesting insights, there was one that caught my attention: Lomuto’s partitioning scheme was discussed as a serious contender (against the universally-used Hoare partition) from an efficiency perspective. Efficiency!
It turns out modern computing architecture does, sometimes, violate common sense.
To Partition, Perchance to Sort
Let’s first recap the two partitioning schemes. Given an array and a pivot element, to partition the array means to arrange elements of the array such that all elements smaller than or equal to the pivot are on the left, and elements greater than or equal to the pivot are on the right. The final position of the pivot would be at the border. (If there are several equivalent pivot values that final pivot position may vary, with important practical consequences; for this discussion, however, we can assume that all array values are distinct.)
Lomuto’s partitioning scheme walks the array left to right maintaining a “read” position and a “write” position, both initially at 0. For each element read, if the value seen by the “read head” is greater than the pivot, it gets skipped (with the read head moving to the next position). Otherwise, the value at the read head is swapped with that at the write head, and both heads advance by one position. When the read head is done, the position of the write head defines the partition. Refer to the nice animation below (from Wikipedia user Mastremo, used unmodified under the CC-BY-SA 3.0 license).

The problem with Lomuto’s partition is that it may do unnecessary swaps. Consider the extreme case of an array with only the leftmost element greater than the pivot. That element will be awkwardly moved to the right one position per iteration step, in a manner not unlike, um, bubblesort.
Hoare’s partitioning scheme elegantly solves that issue by iterating concomitantly from both ends of the array with two “read/write heads”. They skip elements that are already appropriately placed (less than the pivot on the left, greater than the pivot on the right), and swap only one smaller element from the left with one greater element from the right. When the two heads meet, the array is partitioned around the meet point. The extreme case described above is handled with a single swap. Most contemporary implementations of quicksort use Hoare partition, for obvious reasons: it does as many comparisons as the Lomuto partition and fewer swaps.
Given that Hoare partition clearly does less work than Lomuto partition, the question would be why ever teach or use the latter at all. Alexander Stepanov, the creator of the STL, authored a great discussion about partitioning and makes a genericity argument: Lomuto partition only needs forward iterators, whereas Hoare partition requires bidirectional iterators. That’s a valuable insight, albeit of limited practical utility: yes, you could use Lomuto’s partition on singly-linked lists, but most of the time you partition for quicksort’s sake, and you don’t want to quicksort singly-linked lists; mergesort would be the algorithm of choice.
Yet a very practical—and very surprising—argument does exist, and is the punchline of this article: implemented in a branch-free manner, Lomuto partition is a lot faster than Hoare partition on random data. Given that quicksort spends most of its time partitioning, it follows that we are looking at a hefty improvement of quicksort (yes, I am talking about industrial strength implementations for C++ and D) by replacing its partitioning algorithm with one that literally does more work.
You read that right.
Time to Spin Some Code
To see how the cookie crumbles, let’s take a look at a careful implementation of Hoare partition. To eliminate all extraneous details, the code in this article is written for long as the element type and uses raw pointers. It compiles and runs the same with a C++ or D compiler. This article will carry along implementations of all routines in both languages because much research literature measures algorithm performance using C++’s std::sort as an important baseline.
/**
Partition using the minimum of the first and last element as pivot.
Returns: a pointer to the final position of the pivot.
*/
long* hoare_partition(long* first, long* last) {
assert(first <= last);
if (last - first < 2)
return first; // nothing interesting to do
--last;
if (*first > *last)
swap(*first, *last);
auto pivot_pos = first;
auto pivot = *pivot_pos;
for (;;) {
++first;
auto f = *first;
while (f < pivot)
f = *++first;
auto l = *last;
while (pivot < l)
l = *--last;
if (first >= last)
break;
*first = l;
*last = f;
--last;
}
--first;
swap(*first, *pivot_pos);
return first;
}
(You may find the choice of pivot a bit odd, but not to worry: usually it’s a more sophisticated scheme—such as median-of-3—but what’s important to the core loop is that the pivot is not the largest element of the array. That allows the core loop to omit a number of limit conditions without running off array bounds.)
There are a lot of good things to say about the efficiency of this implementation (which you’re likely to find, with minor details changed, in implementations of the C++ or D standard library). You could tell the code above was written by people who live trim lives. People who keep their nails clean, show up when they say they’ll show up, and call Mom regularly. They do a wushu routine every morning and don’t let computer cycles go to waste. That code has no slack in it. The generated Intel assembly is remarkably tight and virtually identical for C++ and D. It only varies across backends, with LLVM at a slight code size advantage (see clang and ldc) over gcc (see g++ and gdc).
The initial implementation of Lomuto’s partition shown below works well for exposition, but is sloppy from an efficiency perspective:
/**
Choose the pivot as the first element, then partition.
Returns: a pointer to the final position of the pivot.
*/
long* lomuto_partition_naive(long* first, long* last) {
assert(first <= last);
if (last - first < 2)
return first; // nothing interesting to do
auto pivot_pos = first;
auto pivot = *first;
++first;
for (auto read = first; read < last; ++read) {
if (*read < pivot) {
swap(*read, *first);
++first;
}
}
--first;
swap(*first, *pivot_pos);
return first;
}
For starters, the code above will do a lot of silly no-op swaps (array element with itself) if a bunch of elements on the left of the array are greater than the pivot. All that time first==write, so swapping *first with *write is unnecessary and wasteful. Let’s fix that with a pre-processing loop that skips the uninteresting initial portion:
/**
Partition using the minimum of the first and last element as pivot.
Returns: a pointer to the final position of the pivot.
*/
long* lomuto_partition(long* first, long* last) {
assert(first <= last);
if (last - first < 2)
return first; // nothing interesting to do
--last;
if (*first > *last)
swap(*first, *last);
auto pivot_pos = first;
auto pivot = *first;
// Prelude: position first (the write head) on the first element
// larger than the pivot.
do {
++first;
} while (*first < pivot);
assert(first <= last);
// Main course.
for (auto read = first + 1; read < last; ++read) {
auto x = *read;
if (x < pivot) {
*read = *first;
*first = x;
++first;
}
}
// Put the pivot where it belongs.
assert(*first >= pivot);
--first;
*pivot_pos = *first;
*first = pivot;
return first;
}
The function now chooses the pivot as the smallest of first and last element, just like hoare_partition. I also made another small change—instead of using the swap routine, let’s use explicit assignments. The optimizer takes care of that automatically (enregistering plus register allocation for the win), but expressing it in source helps us see the relatively expensive array reads and array writes. Now for the interesting part. Let’s focus on the core loop:
for (auto read = first + 1; read < last; ++read) {
auto x = *read;
if (x < pivot) {
*read = *first;
*first = x;
++first;
}
}
Let’s think statistics. There are two conditionals in this loop: read < last and x < pivot. How predictable are they? Well, the first one is eminently predictable—you can reliably predict it will always be true, and you’ll only be wrong once no matter how large the array is. Compiler writers and hardware designers know this, and design the fastest path under the assumption loops will continue. (Gift idea for your Intel engineer friend: a doormat that reads “The Backward Branch Is Always Taken.”) The CPU will speculatively start executing the next iteration of the loop even before having decided whether the loop should continue. That work will be thrown away only once, at the end of the loop. That’s the magic of speculative execution.
Things are quite a bit less pleasant with the second test, x < pivot. If you assume random data and a randomly-chosen pivot, it could go either way with equal probability. That means speculative execution is not effective at all, which is very bad for efficiency. How bad? In a deeply pipelined architecture (as all are today), failed speculation means the work done by several pipeline stages needs to be thrown away, which in turn propagates a bubble of uselessness through the pipeline (think air bubbles in a garden hose). If these bubbles occur too frequently, the loop produces results at only a fraction of the attainable bandwidth. As the measurements section will show, that one wasted speculation takes away about 30% of the potential speed.
How to improve on this problem? Here’s an idea: instead of making decisions that control the flow of execution, we write the code in a straight-line manner and we incorporate the decisions as integers that guide the data flow by means of carefully chosen array indexing. Be prepared—this will force us to do silly things. For example, instead of doing two conditional writes per iteration, we’ll do exactly two writes per iteration no matter what. If the writes were not needed, we’ll overwrite words in memory with their own value. (Did I mention “silly things”?) To prepare the code for all that, let’s rewrite it as follows:
for (auto read = first + 1; read < last; ++read) {
auto x = *read;
if (x < pivot) {
*read = *first;
*first = x;
first += 1;
} else {
*read = x;
*first = *first;
first += 0;
}
}
Now the two branches of the loop are almost identical save for the data. The code is still correct (albeit odd) because on the else branch it needlessly writes *read over itself and *first over itself. How do we now unify the two branches? Doing so in an efficient manner takes a bit of pondering and experimentation. Conditionally incrementing first is easy because we can always write first += x < pivot. Piece of cake. The two memory writes are more difficult, but the basic idea is to take the difference between pointers and use indexing. Here’s the code. Take a minute to think it over:
for (; read < last; ++read) {
auto x = *read;
auto smaller = -int(x < pivot);
auto delta = smaller & (read - first);
first[delta] = *first;
read[-delta] = x;
first -= smaller;
}
To paraphrase a famous Latin aphorism, explanatio longa, codex brevis est. Short is the code, long is the ‘splanation. The initialization of smaller with -int(x < pivot) looks odd but has a good reason: smaller can serve as both an integral (0 or -1) used with the usual arithmetic and also as a mask that is 0 or 0xFFFFFFFF (i.e. bits set all to 0 or all to 1) used with bitwise operations. We will use that mask to allow or obliterate another integral in the next line that computes delta. If x < pivot, smaller is all ones and delta gets initialized to read - first. Subsequently, delta is used in first[delta] and read[-delta], which really are syntactic sugar for *(first + delta) and *(read - delta), respectively. If we substitute delta in those expressions, we obtain *(first + (read - first)) and *(read - (read - first)), respectively.
The last line, first -= smaller, is trivial: if x < pivot, subtract -1 from first, which is the same as incrementing first. Otherwise, subtract 0 from first, effectively leaving first alone. Nicely done.
With x < pivot substituted to 1, the calculation done in the body of the loop becomes:
auto x = *read; int smaller = -1; auto delta = -1 & (read - first); *(first + (read - first)) = *first; *(read - (read - first)) = x; first -= -1;
Kind of magically the two pointer expressions simplify down to *read and *first, so the two assignments effect a swap (recall that x had been just initialized with *read). Exactly what we did in the true branch of the test in the initial version!
If x < pivot is false, delta gets initialized to zero and the loop body works as follows:
auto x = *read; int smaller = 0; auto delta = 0 & (read - first); *(first + 0) = *first; *(read - 0) = x; first -= 0;
This time things are simpler: *first gets written over itself, *read also gets written over itself, and first is left alone. The code has no effect whatsoever, which is exactly what we wanted.
Let’s now take a look at the entire function:
long* lomuto_partition_branchfree(long* first, long* last) {
assert(first <= last);
if (last - first < 2)
return first; // nothing interesting to do
--last;
if (*first > *last)
swap(*first, *last);
auto pivot_pos = first;
auto pivot = *first;
do {
++first;
assert(first <= last);
} while (*first < pivot);
for (auto read = first + 1; read < last; ++read) {
auto x = *read;
auto smaller = -int(x < pivot);
auto delta = smaller & (read - first);
first[delta] = *first;
read[-delta] = x;
first -= smaller;
}
assert(*first >= pivot);
--first;
*pivot_pos = *first;
*first = pivot;
return first;
}
A beaut, isn’t she? Even more beautiful is the generated code—take a look at clang/ldc and g++/gdc. Again, there is a bit of variation across backends.
Experiments and Results
All code is available at https://github.com/andralex/lomuto.
To draw a fair comparison between the two partitioning schemes, I’ve put together a quicksort implementation. This is because most often a partition would be used during quicksort. For the sake of simplification, the test implementation omits a few details present in industrial quicksort implementations, which need to worry about a variety of data shapes (partially presorted ascending or descending, with local patterns, with many duplicates, etc). Library implementations choose the pivot carefully from a sample of usually 3-9 elements, possibly with randomization, and have means to detect and avoid pathological inputs, most often by using Introsort.
In our benchmark, for simplicity, we only test against random data, and the choice of pivot is simply the minimum of first and last element. This is without loss of generality; better pivot choices and adding introspection are done the same way regardless of the partitioning method. Here, the focus is to compare the performance of Hoare vs. Lomuto vs. branch-free Lomuto.
The charts below plot the time taken by one sorting operation depending on the input size. The machine used is an Intel i7-4790 at 3600 MHz with a 256KB/1MB/8MB cache hierarchy running Ubuntu 20.04. All builds were for maximum speed (-O3, no assertions, no boundcheck for the D language). The input is a pseudorandom permutation of longs with the same seed for all languages and platforms. To eliminate noise, the minimum is taken across several epochs.
The results for the D language are shown below, including the standard library’s std.sort as a baseline.
The results for C++ are shown in the plots below. Again the standard library implementation std::sort is included as a baseline.
One important measurement is the CPU utilization efficiency, shown by Intel VTune as “the micropipe”, a diagram illustrating inefficiencies in resource utilization. VTune’s reports are very detailed but the micropipe gives a quick notion of where the work goes. To interpret a micropipe, think of it as a funnel. The narrower the exit (on the right), the slower the actual execution as a fraction of potential speed.
The micropipes shown below correspond to the Hoare partition, Lomuto partition (in the traditional implementation), and branch-free Lomuto partition. The first two throw away about 30% of all work as bad speculation. In contrast, the Lomuto branchless partition wastes no work on speculation, which allows it a better efficiency in spite of more memory writes.
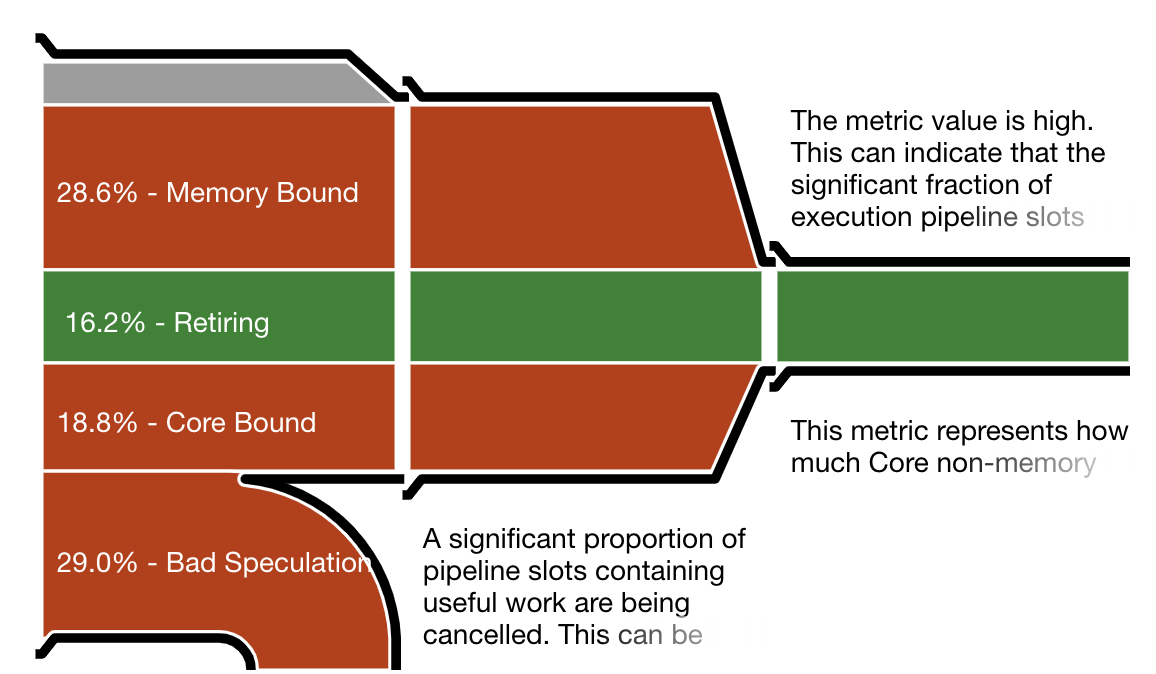
Intel VTune pipe efficiency diagram for the Hoare partition. A large percentage of work is wasted on failed speculation.
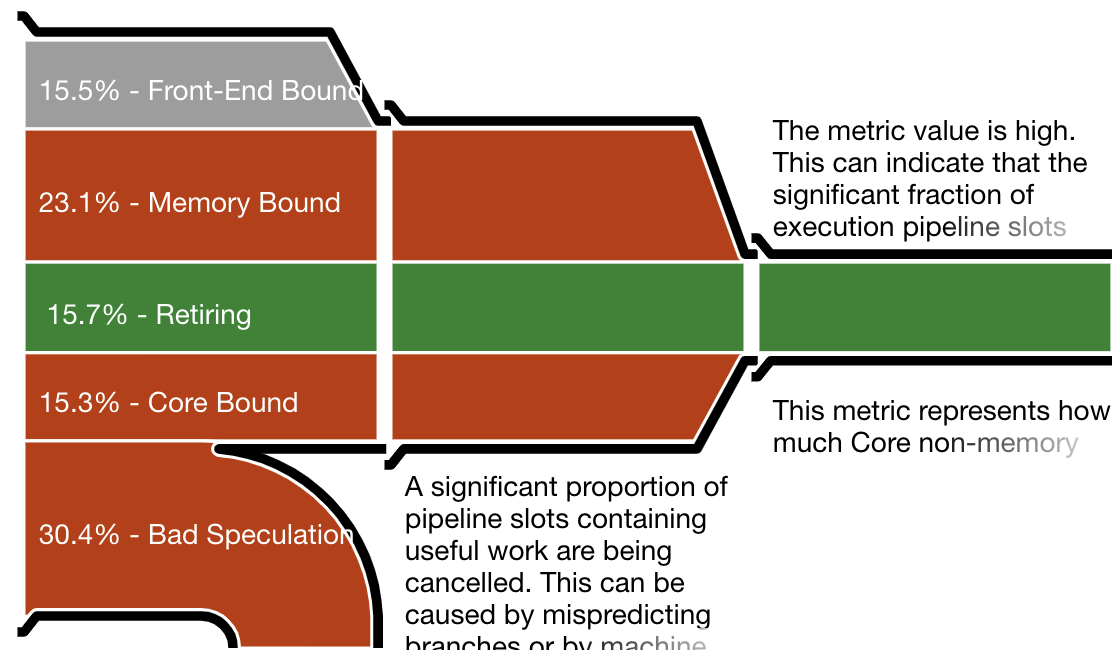
Intel VTune pipe efficiency diagram for the traditional “branchy” Lomuto partition, featuring about as much failed speculation as the Hoare partition.
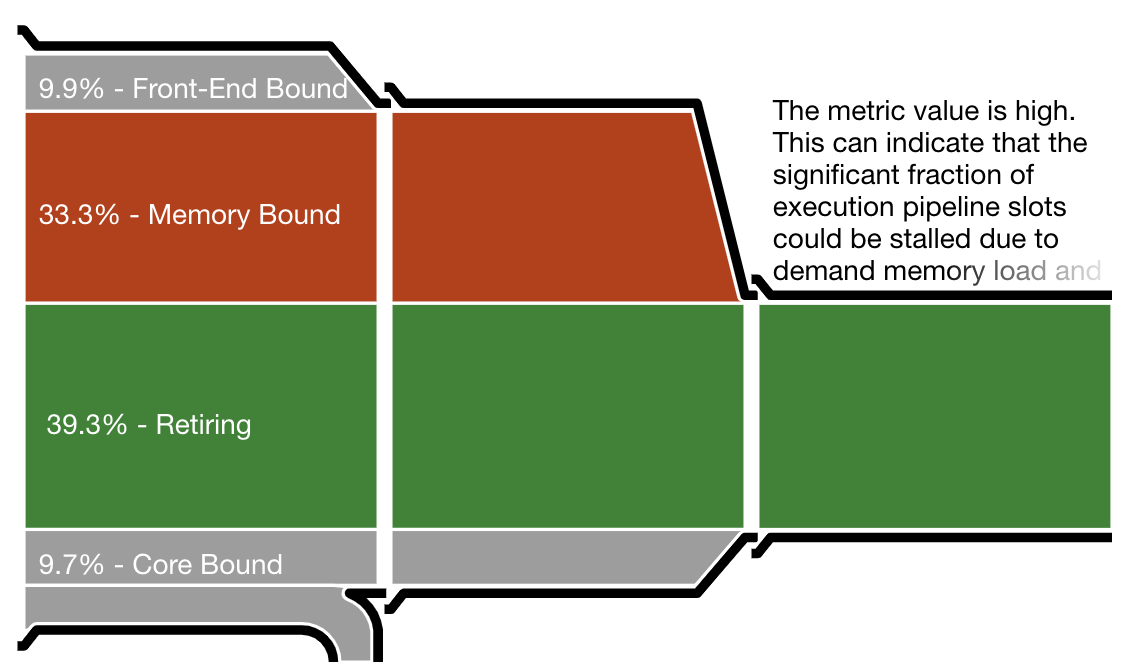
Intel VTune pipe efficiency diagram for the Lomuto branch-free partition. Virtually no work is wasted on failed speculation, leading to a much better efficiency.
Discussion
The four versions (two languages times two backends) exhibit slight variations due to differences in standard library implementations and backend versions. It is not surprising that minute variations in generated code are liable to create measurable differences in execution speed.
As expected, the “branchy” Lomuto partition compares poorly with Hoare partition, especially for large input sizes. Both are within the same league as the standard library implementation of the sort routine. Sorting using the branchless Lomuto partition, however, is the clear winner by a large margin regardless of platform, backend, and input size.
It has become increasingly clear during the past few years that algorithm analysis—and proposals for improvements derived from it—cannot be done solely with pen and paper using stylized computer architectures with simplistic cost models. The efficiency of sorting is determined by a lot more than counting the comparisons and swaps—at least, it seems, the predictability of comparisons must be taken into account. In the future, I am hopeful that better models of computation will allow researchers to rein in the complexity. For the time being, it seems, algorithm optimization remains hopelessly experimental.
For sorting in particular, Lomuto is definitely back and should be considered by industrial implementations of quicksort on architectures with speculative execution.
Acknowledgments
Many thanks are due to Amr Elmasry, Jyrki Katajainen, and Max Stenmark for an inspirational paper. I haven’t yet been able to engineer a mergesort implementation (the main result of their paper) that beats the best quicksort described here, but I’m working on it. (Sorry, Sorters Anonymous… I’m still off the wagon.) I’d like to thank to Michael Parker and the commentators at the end of this post for fixing many of my non-native-speaker-isms. (Why do they say “pretend not to notice” and “pretend to not notice”? I never remember the right one.) Of course, most of the credit is due to Nico Lomuto, who defined an algorithm that hasn’t just stood the test of time—it passed it.
